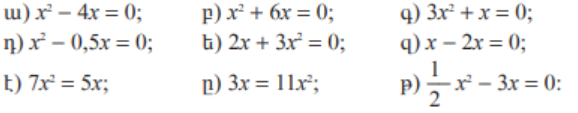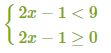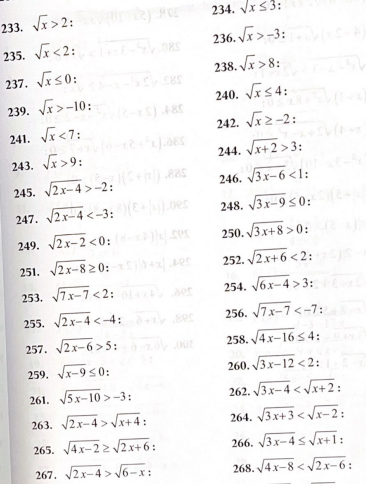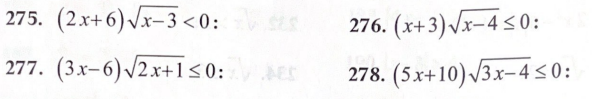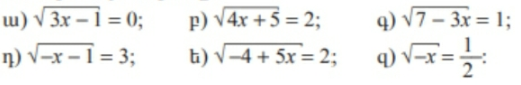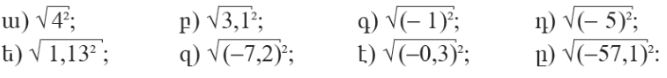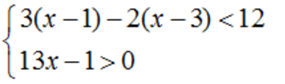Պարապմունք 54․

Թեմա՝ Ընդհանուր տեսքի քառակուսային հավասարումներ։

ax²+bx+c=0 տեսքի հավասարումը, որտեղ a -ն, b -ն և c -ն իրական թվեր են, և a≠0, կոչվում է քառակուսային հավասարում:

Քառակուսային հավասարման արմատները հաշվում են հետևյալ բանաձևերով՝

x₁=−b+√D/2⋅a, x₂= −b−√D/2⋅a, որտեղ D=b²−4ac

D -ն անվանում են քառակուսային հավասարման տարբերիչ կամ դիսկրիմինանտ:

Քառակուսային հավասարման արմատների գոյության հարցը և դրանց քանակը կախված D տարբերիչի արժեքից:

1) Եթե D<0 (բացասական է), ապա քառակուսային հավասարումը արմատներ չունի:

2) Եթե D=0, ապա քառակուսային հավասարումն ունի ճիշտ մեկ արմատ:

3) Եթե D>0 (դրական է), ապա քառակուսային հավասարումն ունի երկու իրարից տարբեր արմատներ:

Օրինակ՝ Լուծենք հետևյալ քառակուսային հավասարումները՝

1) 3x²−5x+4=0

2)25x²−10x+1=0

3) x²−6x+5=0

4) 2x²−4x−3=0

Լուծումներ:

1) Հաշվենք 3x²−5x+4=0 հավասարման տարբերիչը՝ D=5²−4⋅3⋅4=25−48=−23<0

Պատասխան՝ հավասարումը արմատներ չունի:

2)Հաշվենք 25x²−10x+1=0 հավասարման տարբերիչը՝ D=10²−4⋅1⋅25=100−100=0

Հավասարումն ունի մեկ արմատ՝ x=−(−10)+√0/2⋅25=10/50=1/5=0.2

Պատասխան՝ x=0.2

3) Հաշվենք x²−6x+5=0 հավասարման տարբերիչը՝ D = (−6)² −4 ⋅1⋅5 =36−20=16>0

Հավասարումն ունի երկու արմատ՝ x_1,2=−(−6)±√16/2=6±4/2

Պատասխան՝ x₁=5,x₂=1

4) Հաշվենք 2x²−4x−3=0 հավասարման տարբերիչը՝ D=4²−4⋅(−3)⋅2=16+24=40>0 Հավասարումն ունի երկու արմատ՝ x_1,2=−(−4)±√40/2⋅2=4±√4⋅10/2=2±√10

Ուշադրություն

Եթե թվերն արմատի տակից դուրս չեն գալիս, դա չի նշանակում, որ հավասարումը լուծում չունի: Այդ դեպքում արմատներն իռացիոնալ թվեր են:

Առաջադրանքներ։

1․ Լուծել հավասարումները․

1) 2x(x+3)=0
x(x+3)=0
x=0
x+3=0
x=0
x=-3
2) (2x-1)^2=0
2x-1=0
2x=1
x=1/2
3) x^2-4=0
x^2=4
x=+-2
x=-2
x=2
4) x^2-2x-3x+6=0
x(x-2)-3(x-2)=0
(x-2)(x-3)=0
x-2=0
x-3=0
x=2
x=3
5) x=-3+-√3^2-4*6*(-1)/2*6=-3+-√9+24=-3+√33/12
x=-3+√33/12
x=-3-√33/12
6)

2․Լուծել հավասարումները․

x₁ = 0,5, x₂ = 1,5
x₁ = -1/3, x₂ = 5/3
x₁ = 1/2, x₂ = 3
x₁ = -1, x₂ = 3/4
x₁ = 4.5, x₂ = 0.5
x₁ = 0.187, x₂ = 1.187
x₁ = 1/2 + √3/2 i, x₂ = 1/2 — √3/2 i
x₁ = -3/2 + 3√3/2 i, x₂ = -3/2 — 3√3/2 i

3․ Լուծել հավասարումները․

x₁ = -3/2, x₂ = -1
x₁ = 3, x₂ = 3
x₁ = -4 x₂ = 1
x₁ = -7/10 + √11/10 i, x₂ = -0.7 — √(11)/10i
x₁ = -2, x₂ = 18

4․ Լուծել հավասարումները․

x₁ = 3/2, x₂ = 3
x₁ = -3, x₂ = -2/3
x₁ = -4/3, x₂ = 1
x₁ = -5/2, x₂ = 2

Պարապմունք 53.

Թեմա՝ Քառակուսային հավասարման գաղափարը։ Թերի քառակուսային հավասարումներ։

ax2+bx+c=0 տեսքի հավասարումը, որտեղ a -ն, b -ն և c -ն տրված թվեր են, և a≠0, անվանում են քառակուսային (քառակուսի) հավասարում:

Օրինակ

2x²+3x−8=0, −3x²+2x+1=0, x²+5x=0, 2x²−4=0, 25x²=0 հավասարումները քառակուսային հավասարումների օրինակներ են:

a թիվն անվանում են ավագ անդամի՝ x² -ու գործակից, b թիվը՝ x -ի գործակից, c -ն՝ ազատ անդամ:

Քանի որ a≠0, ապա ցանկացած քառակուսային հավասարում ունի ax² ավագ անդամը: Այդ պատճառով քառակուսային հավասարումն անվանում են նաև երկրորդ աստիճանի հավասարում:

Քառակուսային հավասարման ուսումնասիրման հարցերում կարևոր դեր է խաղում հետևյալ թիվը՝ D=b²−4ac

D=b²−4ac թիվն անվանում են ax²+bx+c=0 քառակուսային հավասարման տարբերիչ կամ՝ դիսկրիմինանտ:

Օրինակ

1) 2x²−3x−5=0 հավասարման մեջ a=2 -ը x² -ու գործակիցն է, b=−3 -ը՝ x -ի գործակիցը, իսկ c=−5 -ը՝ ազատ անդամը: Հաշվենք տարբերիչը` D=(−3)²−4⋅2⋅(−5)=9+40=49

2) x²−7=0 հավասարման մեջ b=0, այդ պատճառով էլ չկա x պարունակող անդամը: x² -ու գործակիցը a=1 -ն է, իսկ ազատ անդամը՝ c=−7: Տարբերիչը հավասար է՝ D=−4⋅(−7)=28

Հիշենք, որ

x անհայտով հավասարման արմատ կամ լուծում անվանում են այն թիվը, որը հավասարման մեջ x -ի փոխարեն տեղադրելով ստացվում է ճիշտ թվային հավասարություն:

Լուծել հավասարումը՝ նշանակում է գտնել նրա բոլոր արմատները կամ ցույց տալ, որ արմատներ չկան:

Ուշադրություն

Եթե ax²+bx+c=0 տեսքի հավասարման մեջ a=0, այսինքն, չկա x2 պարունակող անդամը, ապա հավասարումը քառակուսային չէ:

Վերջին երեք օրինակներում a≠0 (այսինքն, դրանք քառակուսային հավասարումներ են), սակայն՝

x²+2x=0 հավասարման մեջ c=0

2x²−6=0 հավասարման մեջ b=0

12x²=0 հավասարման մեջ երկուսն էլ զրո են՝ b=0, c=0

Այս օրինակներում բերվածները կոչվում են թերի հավասարումներ:

Քառակուսային հավասարումը կոչվում է թերի, եթե b և c թվերից գոնե մեկը հավասար է զրոյի:

Օրինակ

Լուծենք հետևյալ թերի հավասարումները՝

1) x²+3x=0

x²+3x=0 x(x+3)=0 x=0 x=−3

Պատասխան՝ x=0,x=−3

2) 2x²−8=0

2x²−8=0 x²−4=0 (x−2)(x+2)=0 x₁=2 x₂=−2

Պատասխան՝ x₁=2,x₂=−2

3) 7x²=0

7x²=0 x²=0 x=0

Պատասխան՝ x=0

Հարցեր և առաջադրանքներ։

1․ Ո՞ր հավասարումն է կոչվում քառակուսային։

2․ Ինչպե՞ս են հաշվում քառակուսային հավասարման տարբերիչը։
D=b²−4ac

3․ Ո՞ր հավասարումն է կոչվում թերի քառակուսային։

Քառակուսային հավասարումը կոչվում է թերի, եթե b և c թվերից գոնե մեկը հավասար է զրոյի:

4․ Կազմել ax²+bx+c=0 քառակուսային հավասարում, եթե նրա գործակիցները հավասար են․

ա) 3x²+4x+5=0
բ) 3x²-2x+6=0
գ) x²-x+2=0
դ) -x²+3x-2=0

5․ Հաշվել քառակուսային հավասարման տարբերիչը․

ա) 49
բ) 21
գ) 0
դ) -3

6․ Ստուգել՝ 0 թիվը հավասարման արմա՞տ է․

ա) այո
բ) ոչ
գ) ոչ
դ) ոչ
ե) այո
զ) ոչ

Լուծել հավասարումները․

ա) x=-1, 1
բ) x=0
գ) x=0, 1
դ) x=-3, 0
ե) x=-2, 3
զ) x=-5, 7
է) x=0, 1/2
ը) x=-2, 0
թ) x=-5, 8
ժ) x=-1, 4

7․ Լուծել հավասարումները․

ա) x=0, 4
բ) x=-6, 0
գ) x=-1/3, 0
դ) x=0, 1/2
ե) x=-2/3, 0
զ) x=0
է) x=5/7, 0
ը) x=3/11, 0
թ) x=0, 6

8․ Լուծել հավասարումները․

ա) x=√3, -√3
բ) x=√5, -√5
գ) x=√3, -√3
դ) x=5√2, -5√2
ե) x=√3/2, -√3/2
զ) x=∅
է) x=48, -48
ը) x=5,6, -5,6
թ) x=200, -200

Protected: Պարապմունք 52

Պարապմունք 51.

Թեմա՝ Պարզագույն իռացիոնալ անհավասարումներ։

Եթե անհավասարման անհայտը գտնվում է քառակուսի արմատի նշանի տակ, ապա այդպիսի անհավասարումը անվանում են իռացիոնալ:

Սովորենք լուծել պարզագույն իռացիոնալ հավասարումները: Պարզագույն իռացիոնալ անհավասարումներն են՝ √x<a և √x>a, որտեղ a -ն տրված իրական թիվ է:

Դիտարկենք √x<a անհավասարումը:

1) Եթե a≤0, ապա թվաբանական քառակուսի արմատի սահմանման համաձայն, անհավասարումը լուծում չունի:

2) Եթե a>0, ապա պետք է անհավասարումը բարձրացնել քառակուսի և պահանջել, որ արմատն իմաստ ունենա (արմատատակ թիվը լինի ոչ բացասական): Եկանք հետևյալ համակարգին՝

Որպես պատասխան ստանում ենք հետևյալ կրկնակի անհավասարումը՝ 0≤x<a²

Դիտարկենք √x>a անհավասարումը:

1) Եթե a<0, ապա ձախից ոչ բացասական թիվ է, իսկ աջից՝ բացասական: Անհավասարումը միշտ ճիշտ է, եթե արմատն իմաստ ունի:

Հետևաբար այս դեպքում անհավասարման պատասխանը ԹԱԲ -ն է՝ [0;+∞)

2) Եթե a≥0, ապա պետք է անհավասարումը բարձրացնել քառակուսի և պահանջել, որ արմատն իմաստ ունենա (արմատատակ թիվը լինի ոչ բացասական): Գալիս ենք հետևյալ համակարգին՝

Որպես պատասխան ստանում ենք հետևյալ անհավասարումը՝ x>a²

Նման ձևով վարվելով՝ կարելի է լուծել պարզագույն ոչ խիստ անհավասարումները:

√x ≤a անհավասարման դեպքում գալիս ենք հետևյալ եզրակացություններին:

1) Եթե a<0, լուծում չկա:

2) Եթե a≥0, ապա x∈[0;a2]

√x ≥ a անհավասարման դեպքում գալիս ենք հետևյալ եզրակացություններին:

1) Եթե a<0, պատասխանը ԹԱԲ -ն է՝ [0;+∞)

2) Եթե a≥0, ապա x∈[a2;+∞)

Օրինակ

Լուծենք √2x−1<3 իռացիոնալ անհավասարումը:

1) Սկզբում գտնենք ԹԱԲ -ը՝ 2x−1≥0

2) Երկու մասերը բարձրացնենք քառակուսի՝ (√2x−1)²❤²

3) Եկանք հետևյալ համակարգին՝

4) Լուծենք ստացված համակարգը՝

5) Պատասխանը ստացված բազմությունների հատումն է՝ x∈[0.5;5)

Առաջադրանքներ։

1․Լուծել անհավասարումները;

233. x∈(4,+∞)
234. x∈(0, 9)
235. x∈(0, 4)
236. x∈(0,+∞)
237. x=0
238. x∈(64,+∞)
239. x∈(0,+∞)
240. x∈(0, 16)
241. x∈(0, 49)
242. x∈(0,+∞)
243. x∈(81,+∞)
244. x∈(7,+∞)
245. x∈(2,+∞)
246. x∈(2, 7/3)
247. ∅
248. x=3
249. ∅
250. x∈(- 8/3,+∞)
251. x∈(4,+∞)
252. x∈(-3, -1)
253. x∈(1, 11/7)
254. x∈(13/6,+∞)
255. ∅
256. ∅
257. x∈(31/2,+∞)
258. x∈(4, 8)
259. x=9
260. x∈(4, 16/3)
261. x∈(2,+∞)
262. x∈(4/3, 3)
263. x∈(8,+∞)
264. ∅
265. x∈(4,+∞)
266. x∈(4/3, 5/2)
267. x∈(10/3, 6)
268. ∅

2․ Լուծել անհավասարումները։

275. ∅
276. x=4
277. x∈(-1/2, 2)
278. x=4/3

Պարապմունք 50.

Թեմա` Պարզագույն իռացիոնալ հավասարումների լուժումը:

Եթե հավասարման անհայտը գտնվում է քառակուսի արմատի նշանի տակ, ապա այդպիսի հավասարումը անվանում են իռացիոնալ:

Կյանքի շատ իրավիճակներ նկարագրվում են իռացիոնալ հավասարումներով: Ուստի, սովորենք լուծել գոնե պարզագույն իռացիոնալ հավասարումները:

Դիտարկենք

Դիտարկենք √2x+1=3 իռացիոնալ հավասարումը:

Ըստ քառակուսի արմատի սահմանման, այն նշանակում է, որ 2x+1=3²: Փաստորեն, քառակուսի բարձրացնելով, տրված իռացիոնալ հավասարումը բերեցինք 2x+1=9 գծային հավասարմանը:

Ուշադրություն

Քառակուսի բարձրացնելը իռացիոնալ հավասարումների լուծման հիմնական եղանակն է:

Դա բնական է, եթե պետք է ազատվել քառակուսի արմատի նշանից:

2x+1=9 հավասարումից ստանում ենք՝ x=4: Սա միաժամանակ 2х+1=9 գծային և √2x+1=3 իռացիոնալ հավասարումների արմատն է:

Քառակուսի բարձրացնելու եղանակը տեխնիկապես բարդ չէ իրականացնել, սակայն երբեմն այն բերում է անցանկալի իրավիճակների:

Օրինակ

Դիտարկենք √2x−5=√4x−7 իռացիոնալ հավասարումը:

Երկու մասերը բարձրացնելով քառակուսի, ստանում ենք՝ (√2x−5)²=(√4x−7)² 2x−5=4x−7

Լուծելով ստացված 2x−4x=−7+5 հավասարումը, ստանում ենք x=1

Սակայն x=1, որը 2x−5=4x−7 գծային հավասարման արմատն է, չի բավարարում տրված իռացիոնալ հավասարմանը: Ինչո՞ւ: Իռացիոնալ հավասարման մեջ փոխարեն տեղադրենք 1: Կստանանք՝ √−3=√−3

Հավասարումը բնականաբար չի բավարարվում, քանի որ հավասարության ձախ և աջ մասերը իմաստ չունե

Ստացել ենք ավելորդ արմատ: Այսպիսի իրավիճակներում ասում ենք, որ x=1 -ը թույլատրելի արժեք չէ, կամ չի պատկանում թույլատրելի արժեքների բազմությանը: Դուրս եկավ, որ այս դեպքում, իռացիոնալ հավասարումը արմատ չունի, մինչդեռ քառակուսի բարձրացնելուց ստացված գծային հավասարումը արմատ ուներ:

Պետք է այսպիսի ավելորդ արմատները ժամանակին հայտնաբերել և չընդգրկել լուծումների մեջ՝ դեն նետել: Դա արվում է ստուգման միջոցով:

Իռացիոնալ հավասարումների համար, ստուգումը լուծման անհրաժեշտ փուլ է, որը օգնում է հայտնաբերել և դեն նետել ավելորդ արմատնելը:

Ուշադրություն

Այսպիսով, իռացիոնալ հավասարումը լուծելու համար պետք է՝

1) այն բարձրացնել քառակուսի,

2) լուծել ստացված հավասարումը,

3) կատարել ստուգում՝ դեն նետելով ավելորդ արմատները,

4) գրել վերջնական պատասխանը:

Կիրառելով այս եզրակացությունը, դիտարկենք հետևյալ օրինակը:

Օրինակ

Լուծենք √5x−16=2 հավասարումը:

1) Երկու մասերը բարձրացնենք քառակուսի՝ (√5x−16)²=2²

2) Լուծենք ստացված հավասարումը՝

5x−16=4 5x=20 x=4

3) Կատարենք ստուգում: √5x−16=2 հավասարման մեջ տեղադրենք x=4: Ստանում ենք՝ √4=2 ճիշտ հավասարությունը:

4) Պատասխան՝ √5x−16=2 հավասարման լուծումը x=4 -ն է:

Հարցեր և առաջադրանքներ։

1․Ո՞ր հավասարումներն են կոչվում իռացիոնալ։

Եթե հավասարման անհայտը գտնվում է քառակուսի արմատի նշանի տակ, ապա այդպիսի հավասարումը անվանում են իռացիոնալ:

2․ Ինչպե՞ս են լուծում պարզագույն իռացիոնալ հավասարումները։

Քառակուսի բարձրացնելը իռացիոնալ հավասարումների լուծման հիմնական եղանակն է:

3․ Լուծել հավասարումները։

ա) x=9

բ) x=0

գ) x=1

դ) x=1/2

ե) x=1/2

զ) x=-1

է) x=44/3

ը) x=1/2

թ) x=7

4․ Լուծել հավասարումները։

ա) x=1/3

բ) x=-1/4

գ) x=2

դ) x=-10

ե) x=8/5

զ) x=-1/4

5․ Լուծել հավասարումները․

249.

x=4

250.

x=9

251

x=25

252

x=4

253

x=0

254

x=81

255.

x=64

256

√x=6+2

√x=8

x=64

257.

√x=1+4

√x=5

258.

√x=0

x=0

259.

√x=2-4

√x=-2

260.

Պարապմունք 47.

Թեմա՝ Եռանկյան մակերեսը (կրկնողություն)։

Առաջադրանքներ։

1․Օգտվելով գծագրից, գտնել ABD, BDC և ABC եռանկյունների մակերեսները։

S_ABD = 72a^2
S_BDC = 96a^2
S_ABC = 168a^2

2․Օգտվելով գծագրից, գտնել ABD, ADC և ABC եռանկյունների մակերեսները։

S_ABD = 48a^2
S_ADC = 32a^2
S_ABC = 16a^2

Օգտվելով գծագրից, գտնել ABC եռանկյան մակերեսը։

S_ABC = 60a^2

4. ABC եռանկյան մեջ ∠C=135^o, AC=6 դմ, իսկ BD բարձրությունը 2 դմ է։ Գտնել ABD եռանկյան մակերեսը։

8դմ^2

5. Երկու եռանկյան բարձրությունները հավասար են, իսկ նրանցից մեկի հիմքը երկու անգամ փոքր է մյուսի հիմքից։ Գտնել այդ եռանկյունների մակերեսների հարաբերությունը։

1:2

Պարապմունք 49.

Թեմա՝ Թվաբանական քառակուսի արմատների հատկությունները։

1․ Պարզեցնել արտահայտությունը․

ա) (2+3)√2=5√2

բ) 4√2-3√2=√2

գ) 1√a-5√a=(1-5)√a=-4√a

դ) 1√x-3√x=(1-3)√x=-2√x

ե) (2+3-4)=√a

զ) √2+3√2×16+1/2√64×2-6√9×2=√2+12√2+4√2-18√2=-√2

2․ Համեմատել արտահայտությունների արժեքները առանց արմատը հաշվելու։

ա) 5√12>3√27

բ) √27<3√2

գ) 2√50>3√32

դ) √3/8<√3/2

3․ Պարզեցնել արտահայտությունը․

ա) √3-1

բ) 5-√5

գ) √3-√2

դ) 4-√10

4․ Հայտարարում ազատվել արմատանշանից։

ա) √2+1

բ) √3+1

գ) 3-√5/2

դ) 2+√3

ե) √3-√2

զ) 4-√15

5․ Կրճատել կոտորակը․

ա) √2

բ) 21/7√3

գ) x

6․ Արտադրիչը տանել արմատանշանի տակ․

Պարապմունք 48․

Թեմա՝ Թվաբանական քառակուսի արմատների հատկությունները։

Դիցուք a≥0, b≥0 և c>0, ապա ճիշտ են հետևյալ հավասարությունները՝

1)√a⋅b=√a⋅√b

2)√a/c=√a/√c

Ցանկացած a իրական թվի համար ճիշտ է՝

3)√a²=|a|

√64⋅81=√64⋅√81−−√=8⋅9=72 √64⋅81=√5184=… =?

Երբեմն հարմար է օգտագործել բերված բանաձևերը հակառակ կարգով, մասնավորապես՝ √a⋅ √b=√a⋅b

Օրինակ՝ Հաշվենք արմատների հետևյալ արտադրյալը՝

√2⋅√32=√2⋅32=√64=8 Պատասխան՝ 8

Ակնհայտ է, որ առանձին 2 և 32 թվերից արմատները չէին հանվում, իսկ արտադրյալից՝ հաջողվեց:

Նման կերպ ենք վարվում, երբ չի հաջողվում առանձին հաշվել արմատների հարաբերությունը:

Օրինակ

Հաշվենք արմատների հարաբերությունը:

√75/√3=√75/3=√25=5

Լինում են իրավիճակներ, երբ թիվը քառակուսի բարձրացնելուց հետո, պահանջվում է արդյունքից արմատ հանել:

Այս դեպքերում կարիք չկա առանձին կատարել երկու գործողությունները՝ պատասխանը միանգամից ստացվում է երրորդ հատկության միջոցով:

Օրինակ՝ Այդպես ենք վարվում հետևյալ օրինակներում՝

√5²=5, √92²=92, √(0.67)²=0.67, √(−1.43)²=1.43

Առաջադրանքներ

1․ Ընտրիր ճիշտ հատկությունները:

√a+√b=√a+b
√a²=a, a≥0
√a: √b=√a:b
√a⋅a =a, a≥0
√a⋅a=a²

2․ Հաշվել․

ա) 6

բ) 12

գ) 20

դ) 35

ե) 90

զ) 560

3․ Հաշվել․

ա) 20

բ) 18

գ) 30

դ) 48

ե) 880

զ) 105

4․ Հաշվել․

ա) 2

բ) 3

գ) x

դ) 1,5x

5․ Հաշվել․

ա) √64=8

բ) √225=15

գ) √900=30

դ) √4900=70

ե) √400=20

զ) √8100000=900

է) √6400000=800

ը) √250000000=5000

6․ Հաշվել․

ա) √16=4

բ) √9.61=3,1

գ) √1=1

դ) √25=5

ե) √1,2769=1,13

զ)

7․ Արտադրիչը դուրս բերել արմատանշանի տակից․

8․ Արտադրիչը դուրս բերել արմատանշանի տակից․

Պարապմունք 45.

Թեմա՝ Մոդուլի նշան պարունակող հավասարումների և անհավասարումների լուծումը։

Հիշենք մոդուլի սահմանումը:

x ոչ բացասական թվի բացարձակ արժեք կամ մոդուլ անվանում են հենց x թիվը՝ |x|=x: Բացասական x թվի մոդուլ կոչվում է նրա հակադիր թիվը՝ |x|=−x

Ավելի կարճ գրում են այսպես՝ |x|={x, եթե x≥0 և −x, եթե x<0

Օրինակ՝ |8|=8 |−3|=−(−3)=3 |0|=0

Մոդուլի հատկությունները

1. |a|≥0

2. |ab|=|a|⋅|b|

3. ∣a/b∣=|a|/|b|

4. |a|²=a²

5. |a|=|−a|

Մոդուլ պարունակող պարզագույն հավասարումներ։

Դիտարկենք |x|=A հավասարումը, որտեղ A-ն իրական թիվ է:

Մոդուլի սահմանումից և հատկություններից հետևում է, որ |x|=A հավասարումը՝

1)A<0 դեպքում լուծում չունի,

2)A=0 դեպքում ունի միակ լուծումը՝ x=0,

3)A>0 դեպքում ունի երկու լուծում՝ x=A և x=−A

Գտնենք y -ը, եթե |2y−1|=3

Այս դեպքը բնորոշ է դիտարկված ընդհանուր դեպքին, եթե համարենք, որ x=2y−1, A=3: Հետևաբար, 2y−1=3 կամ 2y−1=−3

Լուծելով այս գծային հավասարումները, ստանում ենք՝

2y−1=3 2y=4 y=2 կամ 2y−1=−3 2y=−2 y=−1

Պատասխան՝ y -ը հավասար է −1 -ի և 2 -ի:

Մոդուլ պարունակող անհավասարումներ։

Դիտարկենք |x|<A անհավասարումը, որտեղ A -ն դրական թիվ է:

Մոդուլի սահմանումից, հատկություններից և երկրաչափական մեկնաբանությունից հետևում է, որ |x|<A անհավասարումը համարժեք է −A<x<A կրկնակի անհավասարմանը:

Գիտենք, որ կրկնակի անհավասարումն էլ իր հերթին համարժեք է գծային անհավասարումների համապատասխան համակարգին՝

Այսպիսով, եթե A>0, ապա լուծել |x|<A անհավասարումը նշանակում է լուծել անհավասարումների {x<A և x>−A համակարգը:

Ամբողջ ասվածը ուժի մեջ է նաև ոչ խիստ անհավասարումների համար՝

|x|≤A ոչ խիստ անհավասարումը լուծելու համար պետք է լուծել ոչ խիստ անհավասարումների {x≤A x≥−A համակարգը:

Օրինակ՝ Լուծենք |5−2x|≤3 անհավասարումը:

1) Օգտվելով մոդուլի |a|=|−a| հատկությունից, շրջենք մոդուլատակ արտահայտությունը, փոխելով նշանները: Հետևաբար, պահանջվող անհավասարումը կարելի է արտագրել այսպես՝ |2x−5|≤3

2)|2x−5|≤3 անհավասարումը փոխարինենք անհավասարումների համակարգով՝

{2x−5≤3 և 2x−5≥−3

3) Լուծենք համակարգի անհավասարումները՝ {2x−5≤3 և 2x−5≥−3 {2x≤8 և 2x≥2 {x≤4 և x≥1 {x∈(−∞;4] x∈[1;+∞)

4)Հատենք ստացված բազմությունները՝ (−∞;4]∩[1;+∞)=[1;4]

5) Պատասխան՝ x∈[1;4]

Մոդուլ պարունակող անհավասարումներ

Դիտարկենք |x|>A անհավասարումը, որտեղ A -ն դրական թիվ է:

Մոդուլի սահմանումից և հատկություններից հետևում է, որ |x|>A անհավասարմանը բավարարում են այն և միայն այն x -երը, որոնք բավարարում են x<A կամ x>−A պայմաններից գոնե մեկին:

Եթե A>0, ապա լուծել |x|>A անհավասարումը նշանակում է լուծել անհավասարումների [x<A կամ x>−A համախումբը:

Ամբողջ ասվածը ուժի մեջ է նաև ոչ խիստ անհավասարումների համար՝

|x|≥A ոչ խիստ անհավասարումը լուծելու համար պետք է լուծել ոչ խիստ անհավասարումների [x<A կամ x>−A համախումբը:

Օրինակ՝ Լուծենք |4x−6|>2 անհավասարումը:

1)|4x−6|>2 անհավասարումը փոխարինենք անհավասարումների համախմբով՝

[4x−6>2 կամ 4x−6<−2

2) Լուծենք համախմբի անհավասարումները՝ [4x−6>2 կամ 4x−6<−2 [4x>8 կամ 4x<4 [x>2 կամ x<1[x∈(2;+∞) կամ x∈(−∞;1)

3)Միավորենք ստացված բազմությունները՝ (−∞;1)∪(2;+∞)

4) Պատասխան՝ x∈(−∞;1)∪(2;+∞)

Առաջադրանքներ։

1․Լուծել հավասարումները․